This is the first of a short series of articles on intonation. Getting guitars to play in tune on every fret up the neck is one of the most common repair tasks, and one of the most critical parts of building new instruments as well. I hope you enjoy the articles. Meanwhile, please visit my website DoolinGuitars.comfor a look at some guitars which not only play in tune all the way to the 22nd fret, but let you get there without learning new hand positions from the Kama Sutra…

The 1997 Healdsburg Guitar Maker’s Festival included a seminar on intonation, a complex topic which always seems to generate confusion and spirited debate. While the gist of the seminar was simple – “intonate the nut” – questions also arose concerning temperament and stretch tuning. In this series of articles, I’d like to present an overview of these intonation topics, summarize the Healdsburg intonation seminar and to suggest a method for tuning guitars once they are properly intonated.

Out of Tune… With What?

To understand the intonation problems common to all instruments, let’s first look at the origin of the twelve-tone chromatic scale and the diatonic Major scale we select from those twelve tones to make the vast majority of music. Why are there 12 keys (and 12 frets to the octave) and why do we use only seven notes to create the tonality for each of them?

Any stretched string vibrates naturally in whole-number divisions of its length, generating a fundamental frequency and a set of overtones whose frequencies are whole-number multiples of that fundamental. The relative strength of all these frequencies in combination over time is perceived as the timbre, or tone quality, of the sound.

The common guitar technique of playing harmonics simply dampens the fundamental, to force the string to vibrate in some whole-number division without vibrating as a whole. The frequencies of these notes are multiples of the open string frequency. Thus, the harmonic at the 12th fret divides the string in two equal parts (2 times the frequency), while the 7th fret harmonic divides it in three parts (3 times the frequency), the 5th fret in four parts (4 times the frequency), the 4th fret in 5 parts (5 times the frequency), and if you crank up the gain you can get further harmonic divisions between the frets up towards the nut.

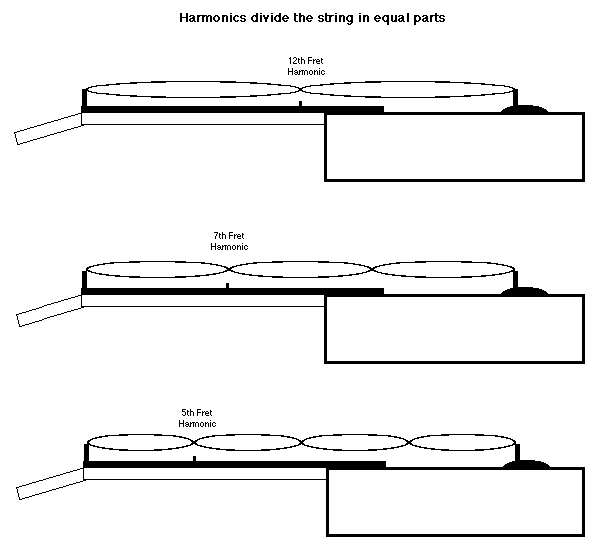
The overtones also describe the seven notes of a scale, albeit spread over several octaves. This scale is similar to our major scale, but oddly enough has a flatted 7th and sharped 4th intervals. In effect, a single vibrating string is singing a whole scale of notes in its harmonic series, and when other strings play notes corresponding to these notes, the result is varying degrees of consonant harmony. Consonance is the result of simple ratios between the frequencies, while dissonance occurs between frequencies having a more complex ratio. Intervals which are perfectly in tune with the Harmonic Series are called Just intervals.

The distances between the notes in this naturally occurring scale happen to fall roughly into whole steps and half steps. If we build a harmonic series from each of these notes we’ll fill in the spaces and generate a 12-tone chromatic scale. Approximately. Because it turns out that the half steps are not all the same size, the whole steps are not all the same size, and the half steps are not exactly half the size of the whole steps. This causes small, but definitely audible discrepancies between the pitch of overtones generated from different fundamental pitches.

The early history of music describes the discovery of these discrepancies and various attempts to cope with them. In fact, with each breakthrough advance in harmony usage, new adjustments, or temperaments, were devised to accommodate the increasing sophistication in harmony.

—————————————————————————————

Intonation II

In this article, I’ll describe the main temperaments and their corresponding musical periods. To compare distances between notes I’ll use cents (pronounced “sonts”), a quantity of pitch change equal to 1/100 of a half-step, or 1/1200 of an octave. This system is very convenient for illustrating the strengths and weaknesses of each temperament, and avoids a lot of hairy math associated with the logarithmic response of the ear to pitch. So here they are, four approaches to producing a set of tones which work together in tune:

Pythagorean Temperament

Named after the Greek mathematician Pythagorus, who discovered the Harmonic Series while experimenting with early string instruments. The scale is built by striking the second harmonic of the string (the harmonic on the 7th fret of the guitar), producing the fifth scale degree, then tuning the string to the new note and striking the second harmonic of that note, etc. around the cycle of fifths. Do this 12 times and you end up where you started… almost. Unfortunately, you actually end up twenty-four cents sharp, or two cents per iteration.

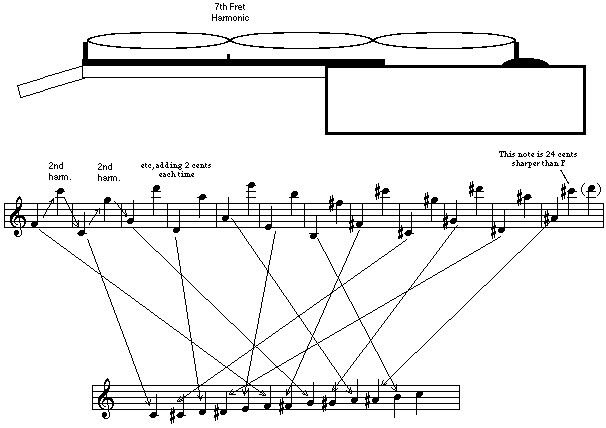
This is what you’re doing when you tune the lower four strings of the guitar by matching the harmonics on the 5th and 7th frets of adjacent strings. It comes pretty close to getting the guitar in tune, since you’ve only gone 6 cents sharp by the time you tune the D string (again, two cents per iteration).

Compared to the Harmonic Series, this scale has very sharp 3rd degrees (22 cents sharper than the Harmonic Series) but the fifth interval is perfectly Just (in tune with the Harmonic Series). This temperament worked great for the parallel fifths in Gregorian chants, but when harmony in thirds became popular those sharp thirds became annoying. To pull the thirds down into agreement, Meantone Temperament was developed.

Meantone Temperament

If you shave a little off of each fifth interval as you generate your scale, you can adjust the intervals in various ways. One popular system shaved five cents from each new interval, resulting in a third scale degree which agrees perfectly with the Harmonic Series. This works beautifully with Renaissance music featuring contrapuntal lines which form thirds. However, if you follow this method all the way around the circle of fifths, you end up 36 cents flat.

Moreover, as soon as someone stacked another third on top to create triads, those slightly flat fifths didn’t sound so great. So why not generate a scale from the beautifully consonant triad from the Harmonic Series?

Just Temperament

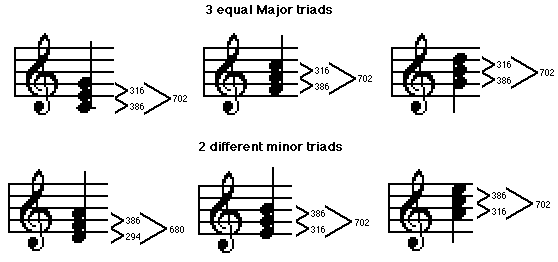
By adjusting the scale tones such that the three major triads in the scale (the I, IV and V chords) all agreed with the Harmonic Series based on their respective roots, a scale results which is perfectly consonant for early triad-based classical music (and modern country-western I suppose).

Unfortunately, Just Temperament produces 2 different sizes of whole steps, and consequently 2 sets of intervals for minor triads. Further discrepancies occur in the chromatic half-steps, making any key more than a couple of sharps or flats away badly out of tune. I, IV and V established true tonality, and along with it, the possibility of contrasting different tonalities – modulation, minor vs. Major keys, borrowing chords from minor within a major tonality, temporary modulations, substitute dominant harmonies, and all the other wonderful devices which twelve-tone harmony offers. Just Temperament offers perfect agreement with the Harmonic Series only in the tones of the I, IV and IV triads and only in the Major key of the I chord.

In fact, none of the above temperaments offers consistent intonation for all keys. The only way to make intonation consistent is to make all of the half step intervals consistent – all the same size. This leads us to…

Equal Temperament

Actually a form of Meantone Temperament, this system shaves just two cents from each fifth around the cycle, which gets you back to exactly the same pitch you started with. As a result, all twelve half steps are exactly the same size so any triad from any scale step also has intervals of the same size. This means that any key, modulation or tonality works as well as any other.

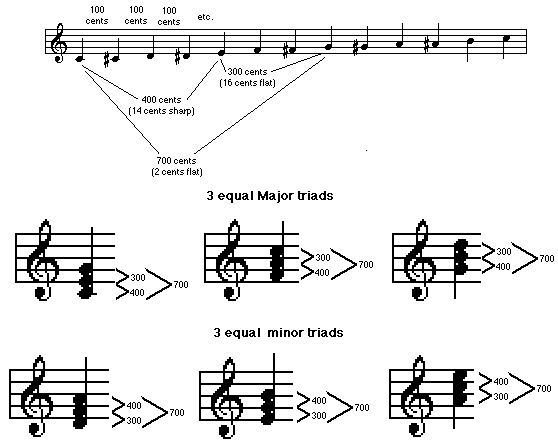
I say “as well as any other” because Equal Temperament has similar problems to those of Pythagorean Temperament – sharp thirds. They’re not as sharp – only fourteen cents rather than twenty-two cents – but sharp enough to sound a bit bright and dissonant compared to “Just” thirds.

————————————————————————————

Intonation III

In Intonation I, I showed how the Harmonic Series implies the 12 tones of our chromatic scale, as well as the discrepancies between the distance between these tones which leads to discrepancies in intonation. Intonation II described the main temperaments and their corresponding musical periods. In this article, I’ll make the case for equal temperament as the best compromize for modern music.

Scales Revisited

As I described in Intonation II, the Harmonic Series creates a seven-tone diatonic scale. This scale hints tantalizingly at a 12-tone chromatic scale by offering two sizes of steps, one roughtly twice the size of the other. By simply filling in a tone halfway between the whole steps, the 12-tone chromatic scale appears.

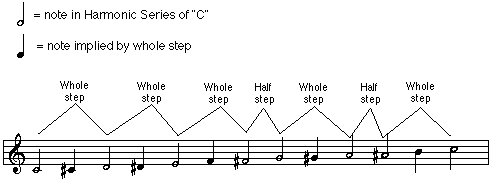
Once we have a 12-tone chromatic scale, we can build a diatonic 7-tone scale from any of those 12 tones by skipping 5 of the 12 to produce the correct sequence of whole- and half-steps. (Note that the Major scale, long ago established as the “home base” for diatonic harmony, has a different pattern of whole- and half-steps than that produced by the Harmonic Series. The reasons for this are way, way beyond the scope of this article.) This produces our familiar system of 12 diatonic key centers. This system is so entrenched in our concept of harmony that the pattern of whole-and half-steps is built into the staff; there is no chromatic step between E and F or between B and C.

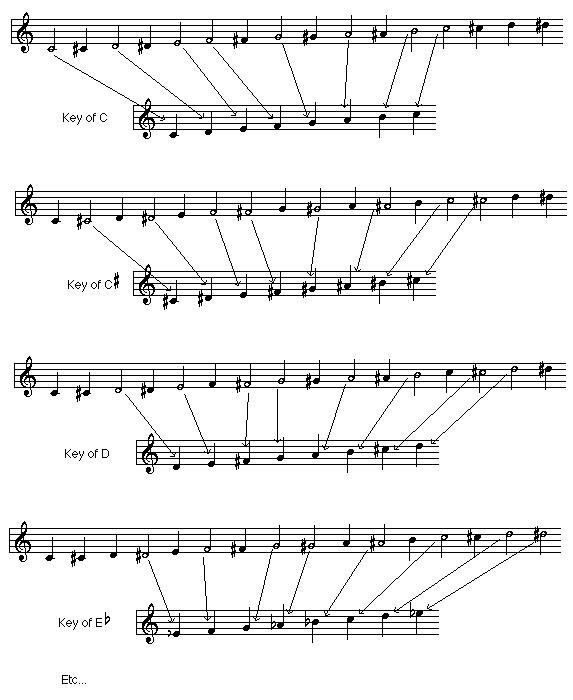
Diatonic harmony creates the powerful sense of tonality by generating the I-IV-V triadic harmony which anchors practically all Western music. Chromatic harmony offers the interest of contrasting tonalities against one another. This system of 7-tones within 12-tones powers virtually every kind of music with any hamonic or melodic content the world over – even Japanese and Indian musics with their microtonal inflections are temperamental variations on this 12-tone system. Moreover, all of the emotional power of harmony to bring a melody to life springs from this structure. It’s hard to overstate this point: Jazz, Country, Classical, Folk, Rock, Pop, Funk, Ambient, Klezmer, Salsa, World, you name it – all of these styles rely on their own characteristic uses of 12-tone harmony for their very existance.

The Illusion of the 12-tone Chromatic Scale

OK, so 12 tones are good. But when we filled in the spaces between the whole-steps we assumed that they were all the same size, and all twice the size of a half-step. Unfortunately, the Harmonic Series didn’t provide us with quite that tidy a package. In fact, the implication of 12 half-steps is a mere mathematical accident! As I showed in Intonation II , some of the steps generated from the Harmonic Series are off by as much as 22 cents – almost a quarter of a half-step. But still, to our ears the implication of 12 tones is real. This has motivated folks down throughout history to devise the various temperamants which I described in Intonation II . However, only one of these temperaments works for all 12 keys, by virtue of making all 12 half-steps exactly the same size: Equal Temperament.

The Case for Equal Temperament

Equal Temperament has had a bad rap since its inception. Baron von Helmholtz, the father of Acoustics as a science, so preferred Just Temperament that he declared that string and vocal groups, performing without reference to a tempered instrument, would automatically play in Just intervals. Modern electronic analysis has proved this false. Performers actually tend towards Pythagorean thirds – even sharper than Equal Temperament thirds!

The fact is, intonation is part of the expressive palette of most instruments. Wind, string and vocal musicians adjust the intonation of each note, and not necessarily to achieve perfect consonance. Guitarists in particular often bend strings for pitch inflection. This is part of the essential tension and release of musical flow. All musicians, regardless of what instrument they play of sing through, must play their instrument in tune, and use intonation as an expressive tool.

The fact is, Equal Temperament is not just a necessary compromise, it’s a very reasonable one in exchange for the rich palette of harmonic expression it provides by making the 12-tone system practical. Pianos, correctly intonated guitars, and any other instruments playing with them conform to it, which accounts for the vast majority of recorded music… I’m talking practically all of the music you’ve ever heard! I often wonder how many of those folks who talk knowingly about the superiority of earlier temperament systems have actually heard music played with those temperaments!

But most importantly for guitarists and luthiers, the spacing of frets on the guitar fretboard is Equal tempered. The only way to achieve another temperament is to make a special “broken Fret” fretboard for each key you wish to use! This may be appropriate for performance of some early music, although not strictly accurate since such fretboards weren’t used at the time.

Meanwhile, I’ll look for your suggestions and questions in my mailbox…

http://www.doolinguitars.com/maillist.html

——————————————————————————

Intonation IV

In  Intonation I, I showed how the Harmonic Series implies the 12 tones of our chromatic scale, as well as the discrepancies in the distance between these tones which lead to discrepancies in intonation. Intonation II described the main temperaments and their corresponding musical periods. In Intonation III, I hope I made the case for equal temperament as the best compromise for modern music. In this article I’d like to show how all of this applies to the guitar.

The Equal Tempered Fretboard

As I mentioned in Intonation III, the spacing of the frets on the guitar fretboard is Equal Tempered. Mathematically this means that each successive fret is closer to the bridge by a factor of the 12th root of 2; that is, the number which when multiplied by itself 12 times equals 2. This isn’t really all that weird – if there are 12 frets to the octave, and the pitch at the octave is twice that of the open string, the 12th root of two simply divides the octave into 12 logarithmically equal parts, satisfying the ear’s logarithmic response to frequency. This explains why the frets get closer together the higher you go, while the pitch difference between each pair of frets is always one half-step.

But more importantly for fretted string instruments, Equal Temperament generates the same fret spacing for any string tuned to any pitch. This allows for straight fret slots which are parallel to the nut – something we’re all accustomed to seeing. Any other temperament system would create some pretty strange-looking frets, since the spacing would vary depending on what interval of the scale occurred at a given fret and string. The frets would be “broken” or “staggered” across the fretboard, and a different placement would be required for each key! Such fretboards have been made in the past; one system I’ve seen used replaceable fretboards to allow the player to switch temperaments for different musical pieces.

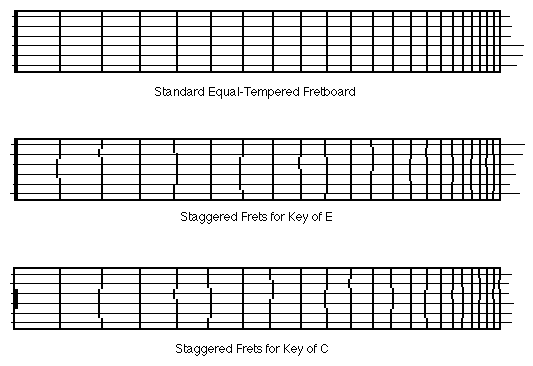
While there may be a place for this sort of thing, the vast majority of guitarists simply want their regular old fretboards to play in tune. The good news is that this isn’t asking too much since the frets of most guitars are placed accurately according to Equal Temperament. The bad news is that most guitars fail to achieve Equal Temperament due to incorrect saddle and nut placement. Let me emphasize this point: before we blame Equal Temperament for the intonation woes of guitars, let’s be sure we’ve actually achieved Equal Temperament in the first place!

To do so, we must do two things: get the saddle and nut placement right, and tune the strings correctly. Saddle and nut placement is the luthier’s responsibility, whether the luthier in question is the original builder of the guitar, a qualified repair person, or the owner of the guitar who does his or her own repairs. Tuning the strings is the player’s responsibility, or in some professional situations, the guitar tech’s. As I will describe below, there is more to these techniques than common knowledge would suggest. In other words, there’s more to guitar intonation than adjusting the saddle, and there’s more to tuning a guitar than 7th fret harmonics and sweet-sounding open-E chords.

Intonation 101

First, a quick review of standard intonation technique. The guitar’s bridge is placed on the top such that the 12th fret is at the midpoint of the strings. This makes the pitch at the 12th fret one octave above that of the open string, or twice the frequency. The nut is placed at the “zero fret” position, and fret positions are calculated from it using the 12th root of 2 formula. Fretting the string shortens its length by some multiple of the 12th root of 2, according to which fret is used, yielding a pitch which is an Equal Tempered interval above the open string’s pitch. The theoretical position of the saddle in the bridge is exactly twice as far from the nut as the 12th fret.

I say “theoretical” because the act of fretting the string bends its pitch sharp, to a degree determined by the gauge and material of the string, action height, scale length and open-string pitch. To compensate for this sharpening, the saddle is moved away from the nut, which lengthens the string to make it sound flatter. Since so many factors affect how sharp the string goes when fretted, there is no standard amount of compensation which works for every guitar. To play in tune, every guitar needs its saddle position fine-tuned for the strings and tuning to be used. On most electric guitars, this is accomplished with individual screw-adjustable saddles, while on most acoustic guitars the bone saddle must be shaped to set the point of string termination within the saddle’s width. Either way, the length of each string is adjusted to compensate for the sharpening of its pitch when fretted.

Intonate the Nut?

OK, that’s how we’ve all been taught to intonate guitars. But does it really do the job? Consider the nut, or open-string pitches. We compensate for the sharpening of pitch due to stretching the strings down to the frets by adding saddle compensation. Well, it’s the same story at the nut: the higher the nut action, the more compensation is needed. What do I mean by nut action? If you imagine the plane of the frets (assuming for a moment that there is no “relief”, a perfectly flat fretboard) running from the last fret to the first, and then extending to the nut, the bottom of each nut slot relative to that plane determines nut action. If the nut slot is cut so it exactly meets the plane of the frets, there is effectively zero nut action. If the slot is cut deeper than that, the open string will certainly buzz on the first fret – time for a new nut. But if the slot is cut more shallowly, so it comes short of the plane of the frets, that distance is what I refer to as nut action. And the shallower the slot, the higher the nut action, the sharper the string goes, and the more nut compensation is needed.

But what does this mean when we tune the guitar by tuning the open strings and intonate the saddle from there? It means that the open strings and the 12th fret are the only pitches which are really in tune! If you test the pitches at each fret of a traditionally intonated guitar, you’ll find that the pitches go progressively sharp as you move backwards from the 12th fret to the nut, and progressively flat as you move up from the 12th fret towards the bridge.

This effect is more subtle than that of an uncompensated saddle, but is significant and quite audible. The solution is nut compensation. Like saddle compensation, the nut is moved away from its theoretical position to change the string length, to varying degrees according to string type and pitch. Since the sharpening effect of high nut action makes the open strings flat relative to the fretted notes, moving the nut closer to the saddle will compensate by shortening the string, so the open string pitches go sharp to the same degree. In other words, the end of the fretboard is shaved slightly short, moving the nut toward the bridge.

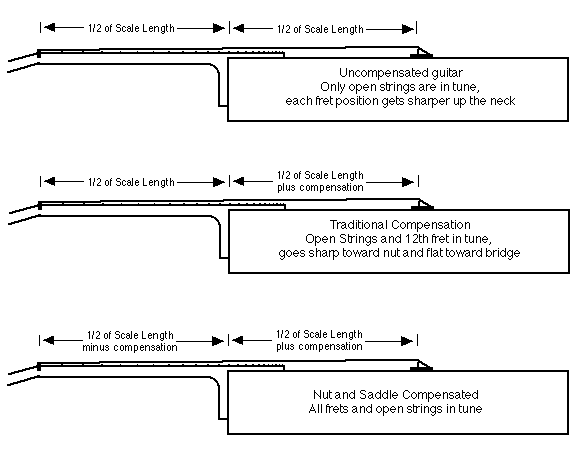
Nut compensation has been researched extensively by two classical luthiers, Greg Byers and John Gilbert. They have taken different approaches to the problem, but both have achieved good results.

John Gilbert’s solution is to shave about one thirty-secondth of an inch from the end of the fretboard, applying the same amount of compensation to all the strings (just as the straight saddle on the classical guitar does at the bridge end). For new designs he accomplishes this by using a longer scale fretboard than the actual scale length, without changing the nut or twelfth fret location. For example, he uses a twenty-six and one-thirty-second inch scale fretboard on a twenty-six inch scale guitar and shaves a bit from the nut end of the fretboard. John has used this system since 1978 with excellent results, as confirmed by his many satisfied clients.

Greg Byers did extensive mathematical modeling of string compensation, which yeilded specific compensations for each string at the nut and saddle. To confirm the results of his theoretical model, he attached a fixed fretboard and movable “nut” and “bridge” sections to a long plank and moved the nut and bridge to find correct nut and saddle compensation. Each string is mounted on the device and the ends are adjusted until each fret and the open string read in tune; the distances to the nut and saddle are then measured and transferred to the instrument. This yields both staggered nut and saddle.

Byer’s method results in individual compensation per string, an improvement over Gilbert’s equal compensation. Both luthiers note, however, that the amount of compensation is slight and that they are both working toward the same end.

Or set the Nut Action?

On my own instruments, I find that if i get the nut action as low as possible for a given instrument and player, I usually don’t need nut compensation. But some setups do require it. The point is to realize what is causing the need for nut compensation (the sharping effect of nut action), and to treat each each instrument individually, compensating only as needed.

As a starting point, I set my nut action to about .010″ on the top four strings and .020″ for the bottom two on steel string guitars, and about double that for nylon string guitars. I do this by measuring the height of the first fret, stacking up feeler gauges to that height plus the nut action desired, slide the feeler gauge stack under the strings up against the nut, and file the slot until the file just touches the feeler gauge. From there, I look at and feel the action at the first fret; if I think I can lower the nut action on any string I do so a few thousandths at a time. Then when the nut action is as low as I feel I can get it, I check the first fret intonation relative to the open strings, and if I’m still seeing any strings going sharp at the first fret, only then will I shave the end of the fretboard.

Meanwhile, I’ll look for your suggestions and questions in my mailbox…

E-Mail Me

——————————————————————————————

Intonation V

In this article I’ll describe a technique for correctly tuning a guitar once it’s correctly intonated, along with some thoughts about alternatives to traditional intonation, and intonation problems between pianos and guitars. I hope you’ve enjoyed the articles. Also, please visit my website www.DoolinGuitars.com for a look at some guitars which not only play in tune all the way to the 22nd fret, but let you get there without having to learn Yo-Yo Ma’s left hand thumb technique…

But I still can’t get my guitar in tune…

Assuming your guitar is completely intonated (frets correctly placed, nut and saddle compensated, good new strings), the instrument is still a challenge to tune. This is because any string may carry any of the 12 possible tones during a given piece, and errors tend to compound. Unfortunately, many players exacerbate the problem by trying to tune to 1st position triads, such as the ever-popular open E chord. In doing so, they’ll tend to tune the A and B strings a touch sharp and the G quite a bit flat, in an attempt to make that E chord sound really good. They’re actually tuning to the harmonic series of the low E, resulting in fifths tuned 2 cents too high and thirds tuned 14 cents flat. Obviously, “tuning to harmonics” has the same problem, since guitar harmonics are isolated pitches from the overtone series of the strings (as discussed in Intonation I).

You can compensate a bit by intentionally tuning the third sharp and the fifth flat, but this is hard to do accurately. I’ve stumbled upon a simple and quick tuning system which avoids thirds entirely:

1. Get the guitar “in the ball park” by tuning to a pitch reference, the 4th and 5th frets, harmonics, or whatever.
2. Check your tuning by playing these two chords, adjusting until they sound equally in tune:

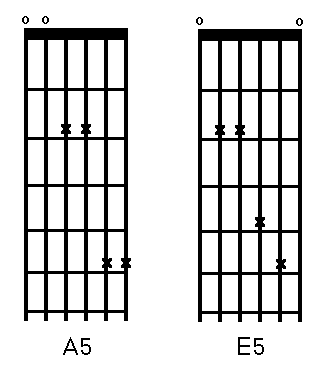
The two chords shown will average out any discrepancies because they only contain roots and fifths, and because the root of one is the fifth of the other and vice versa. Since these chords contain only fifth and fourth intervals, and since an Equal Temperament fifth is two cents sharp and an Equal Temperament fourth is two cents flat, tuning this way splits any difference; the thirds are automatically in tune (to the Equal Tempered scale) due to fret placement.

This should give you a guitar which conforms to Equal Temperament within the limitations of real-world strings and fret placement, which is pretty darn close. This means that any combination of notes anywhere on the neck should yield Equal Tempered intervals and chords, and will agree with any other instrument tuned to Equal Temperament. Unfortunately, we cannot include in this group of instruments the other great polyphonic instrument of Western music, the Piano.

What About Stretch Tuning?

While the basis of piano tuning is Equal Temperament, the behavior of real-world strings doesn’t conform to that tidy theory. Way back in Intonation I, I showed how a string vibrates in whole-number divisions of its length, generating a fundamental frequency and a set of overtones whose frequencies are whole-number multiples of that fundamental. In reality, these pitches can vary considerably from that ideal due to the phenomenon of inharmonicity. The overtones of real-world strings are always a bit sharp due to the stiffness of the string – each smaller subdivision of the string’s length requires a sharper deviation from the straight line, bending the pitch sharp.

Inharmonicity is a pronounced and crucial element of piano tone in particular, but is present and important in guitar tone also. The reason for this difference in the degree of inharmonicity between the instruments is due to the great difference in length, diameter and tension of their strings. Any given piano string may be carrying as much or more tension as all six strings on a guitar! The smaller, lower tension strings of the guitar produce a truer overtone series, and the guitar’s relatively louder fundamental tones tend to mask discrepancies.

The greater inharmonicity in pianos creates a strange problem with their tuning. If a piano is simply tuned to Equal Temperament across its range, the clash between the markedly sharp overtones of the low strings and the fundamentals of the high strings make the instrument sound out of tune with itself! The solution: “stretch tuning”, wherein the high and low registers of the piano are tuned higher and lower, respectively, to bring the low strings’ harmonics into tune with the upper strings’ fundamentals. Thus, the piano is intentionally tuned out of Equal Temperament, in order to sound in tune with itself. (Note that this has nothing to do with temperament, which refers to the spacing of tones within the octave, regardless of register.)

Happily for guitarists and pianists playing together, the stretch is not applied linearly; most of it occurs in the 1-1/2 octaves above and below the guitar’s range. At the open low E and the 19th fret of the high E, the stretch is only about 5 cents, while anywhere on the top three strings up to the 12th fret is within 2 cents. The open high E is exactly in tune with the piano. While we’re only talking about 2-1/2 cents per octave, the discrepancy is there, and shows why pianos and guitars can’t ever be perfectly in tune with one another.

Alternative Intonation Systems

This problem of pianos and guitars has given rise to alternative intonation systems which attempt to bring the two instruments into agreement. These systems usually employ some variant of nut and saddle compensation, and/or stretched positioning of the higher frets, to simulate the stretch tuning of pianos. While it may be that a guitar set up in this manner could play in better tune with a piano, it cannot be in tune with itself, at least within the realm of Equal Temperament. Achieving Equal Temperament across the whole neck is the best all-purpose intonation solution.

But Those Thirds Sound So Sharp…

OK, I’ll admit that even I have a hard time listening to those Equal Tempered thirds sometimes. And sometimes, I’ll cheat, just a little, to get the effect of Just Temperament out of an Equal Tempered guitar.

The way do this is to reserve a string for the third of the chord, tune that string down a bit, and play around it the rest of the time. The simplest example is to tune the open E chord to Just intervals, and play barre chord versions of that chord up and down the neck. As long as you only play that Major chord shape, it will be in Just Temperament everywhere on the neck. This may sound pretty limiting, and it is, but it’s a trick that’s been successfully used on thousands of studio recordings.

This idea can be expanded upon by refingering more complex pieces of music so that the third always falls on the same string, moving anywhere on the neck to make that happen.

Much beyond this though, and you’ll start thinking about split frets, more than 12 frets per octave, B-Benders, pedal-steel style string stretchin’ contraptions, hexaphonic pickups with hexaphonic harmonizers and MIDI presets to track your momentary temperament desires, DSP plug-ins and all-night digital editing sessions in the studio… beyond here lies madness.

—————————————————————————————-

Intonation VI

I got a call from one of my readers that made it clear to me that I’d screwed up: I had spent so much time explaining the details, I hadn’t got the big point across. This has to be the worst sin a technical writer can commit. So for those of you who have understood everything so far, I apologize for beating a dead horse. But for those of you who were left scratching your heads after 5 articles of reading, I’d like to resurrect this poor steed and give it one more good whack.

Intonation 0.5

It’s not that I completely left out the crux of my argument, I just didn’t give it enough emphasis. So, quoting from Intonation IV, here it is:

“… the act of fretting the string bends its pitch sharp, to a degree determined by the gauge and material of the string, action height, scale length and open-string pitch.”

I’d like to fine-tune that explanation just a bit by adding the following:

The relative intonation of any note on the guitar is determined by the position of that fret relative to the nut and saddle, and how much that string is bent sharp by fretting that note.

It’s a problem in two dimensions. Horizontally, the relative placement of the nut, frets and saddle lay out the equal-tempered scale. Vertically, the distance from each string to each fret determines how much the string goes sharp when fretted.

New Horizons

As I explained in Intonation IV, fret placement is calculated mathematically according to a division of the octave into 12 logarithmically equal parts. The scale length is first established by the distance from the nut to the saddle. Then that scale length is divided by the 12th root of 2 (1.05946…) to locate the first fret. Each successive fret is located by dividing the remainder of the scale length by that number. When you get to the 12th fret, you have divided by the 12th root of two, 12 times, which is to say you’ve divided by two. Halving the length doubles the pitch, giving you a perfect octave at the 12th fret.

The fretboard is slotted for the frets according to this formula, and most modern luthiers and guitar factories cut the slots to a very high degree of accuracy, so let’s assume that the frets on most any fretboard are correctly placed. But the fret slot positions are calculated relative to the nut, so all of this careful fret placement is for nought if the nut is incorrectly placed.

Ignoring the factor of strings bending sharp when fretted, let’s look at an extreme case of nut misplacement. Let’s suppose that I were so careless as to cut 3/4″ off the nut end of the fretboard. Now the nut is actually about halfway between its correct position and the first fret. I’ve drawn a little mark on the string to show where the fret should contact it relative to a correctly placed nut:

If I were then to intonate this guitar by the traditional method of comparing the harmonic at the 12th fret with the fretted pitch there, I might think everything was be fine. But the fact is, every note below the 12th fret will be flat, and every note above the 12th fret will be sharp! This is an extreme example, but misplacing the nut by a few thousandths of an inch can audibly throw off intonation.

So nut placement is critical to the intonation of every note on the neck, not just the open strings. But what is correct nut placement? As I explained in Intonation IV, the nut placement must be compensated because the open strings are the only notes on the neck that are not fretted, and therefore are not bent sharp. This is why the nut must actually be placed slightly closer to the saddle than the mathematical ideal.

————————————————————————————-

Intonation VII

I’ve described how the nut, frets and bridge saddle must be in correct relative position for the guitar to play in tune. But in our 2-dimensional intonation problem, the height of each string above each fret is the other factor affecting intonation. Let’s talk what happens when you bend the string by fretting it, on a guitar whose fretboard is less than perfectly straight.

Let’s assume that we have a guitar whose nut, frets and saddle are placed at the theoretical ideal. That is to say, the frets are placed relative to one another according to the 12th root of 2 formula, and the nut and saddle are compensated to account for the general tendency for a string to go sharp when bent out of a straight line (all described in Intonation VI). One might think that the guitar should play perfectly in tune, right? Unfortunately, there are still at least three factors that may cause some notes to play out of tune:

1. Variations in relative height of a string above each fret
2. Variations in a string properties along its length
3. Body resonances in the guitar itself

How Straight is Straight?

We all know that bending a string out of a straight line raises its pitch, and we’ve seen that we do just that by simply fretting a note. That’s why the nut and saddle must be compensated. But nut and saddle compensation apply globally to every fret along a given string.

For example, filing the saddle back a little under the high E string moves that string’s saddle contact point away from every fret, and therefore compensates each fret by the same distance. Since the frets get closer together as you move up the fretboard, this distance of compensation is more significant the closer the frets get to one another. The 1st fret is compensated very little, but each successive fret gets a little bit more compensation up to the last fret, which gets the most compensation. This is just dandy, because the string gets further away from each successive fret as you go up the neck, so each successive note actually needs a bit more compensation than the last.

So if we assume a gradual and consistent increase in distance from each successive fret to the string, the saddle compensation applies correctly to each fret, and every note plays in tune. But what if this increase in distance is not gradual and consistent? If the neck has a dip or a hollow in it, or if one fret is worn more than its neighbors, the distance between the string and a given fret may be more or less than expected for the given compensation. And clearly, bending the string more or less means more or less sharpening of the pitch: a note that isn’t in tune.

This is the kind of intonation problem found on older instruments whose necks have warped over time and whose frets need work. The solution is a complete refret, where the frets are removed, the fretboard is planed true, and new frets are installed, leveled and crowned. Players are often pleasantly surprised to find that a complete refretting not only makes their old friend play without buzzes, but play better in tune.

Change Those Old Ropes!

Modern guitar strings are a marvel of technology. We all take for granted that we can go to the corner music store and buy a high E string that’s exactly .012″ in diameter along its entire 30″ length, and that’s a pretty remarkable feat, especially for less than the price of a cup of coffee! But your guitar’s intonation depends upon the perfect consistency of the diameter, tensile strength and density of each string, as it is exactly those properties which make it vibrate predictably.

The above is the “best case scenario”, with a brand new set of strings. Fretting the string permanently kinks it slightly at each fret. Finger oils accumulate in the windings, thereby increasing its mass, but only where you actually touched the string. Abrasion and corrosion wears away tiny bits of the string’s surface in similar places on the string. After playing them a bit, our technological marvels have entered the real world, and are no longer performing quite up to specs. If a guitar won’t play in tune, the first thing to try is a new set of strings, and maybe a different brand or gauge, since they all intonate differently.

But even a brand new string has limitations. Any string gauge plays best in tune within a relatively limited range of scale length and tension. This is why medium gauge strings usually play better in tune that extra lights: a medium set on a guitar with standard scale length in standard tuning is in its optimum range to play in tune (that’s also why it’s so hard to bend blues notes on a medium set). The extra light set is really a bit floppy when tuned to standard tuning, so it’s easy to play those blues bends, but also easy to unintentionally bend a note out of tune. This set is at a shorter scale length, or a lighter gauge, or a lower pitch, than optimum for intonation purposes; those gauges could play better in tune with a longer scale length or a higher pitched tuning.

At the other extreme, a heavy string gauge at high tension may run into another limitation: the stiffness of the string itself. One of my readers is exploring chordal playing in the high reaches of the bass guitar and is having a lot of intonation difficulties. While I have advised him how to adjust the instrument, I suspect that the stiffness of standard bass strings at such a short effective scale length (played well above the 12th fret) may cause them to play sharper than standard intonation techniques can compensate for. In fact, I have found it nearly impossible to intonate a medium-gauge low E string on a guitar so that it plays in tune above the 12th fret, while still playing in tune lower on the neck. String stiffness is a reality that unfortunately may limit what we can do at the extremes of our instrument’s ranges.

————————————————————————————-

I have a client whose ears are a phenomenon of nature. She can hear intonation discrepancies that I have to strain to discern. This remarkable ability is both a blessing and a curse: she sings absolutely perfectly in tune, and tunes her guitars perfectly by ear, but little intonation discrepancies in her guitars drive her nuts! Having her as a client has motivated much of my investigations into guitar intonation. I’m happy to say that she’s more satisfied with the intonation of her Doolin Guitar than any other she owns, and believe me, I had to work pretty hard to achieve that distinction.

She brought me a very nice Martin “M” model which she had played for years. She had taken it to a good repairman who had trued the fretboard, refretted the neck, and compensated the saddle, but it still sounded wrong to her so she brought it to me to see if I could do any better. I agreed that it wasn’t playing in tune, so I did a detailed intonation study of every fret on every string.

What I found surprised me so much that I borrowed another Martin (a dreadnought) and did the same intonation study, with the same results:

1. All the strings were in tune at the 12th fret, and reasonably close at every other fret, except
2. at the 2nd, 3rd and 4th frets, the low E was quite sharp and
3. at the very same frets, the A was quite flat!

This completely blew my mind. I checked the fret placement, and it matched my precision fretting template perfectly. There was no excessive fret wear or neck warpage since the guitar was newly refretted. I tried several brand-new sets of strings and got the same results, from both guitars. How could different strings be out of tune in opposite directions at the same few frets, when they were both in tune above and below those frets? I would have thought that the fret would have to be slanted or staggered to accomplish that.

I did the same detailed intonation study of one of my guitars, and every fret played in tune, no exceptions. I’m not saying this to prove that I make a better guitar than Martin, I only mean to say that something I was doing saved my guitar from this anomaly that was common to both of the Martins I studied. So what was I doing different?

All I can do is speculate, but I believe that the problem was resonances in the necks of those two Martins. I inlay two strips of graphite in my necks, one on either side of the truss rod. Graphite is about 15 times stiffer than wood for the same amount of material, and stiffer means higher frequency. I speculate that the Martin necks had resonances close to the notes that were playing out of tune, and that those resonances were pulling those notes sharp or flat. I knew that graphite would make my necks more resistant to warpage, and had noticed that it prevented “dead spots” as well – every note on my guitars has about the same tone color and sustain. I think that the graphite also raises the resonant frequencies of my necks above the fundamental frequencies of the notes on the neck. Since the neck doesn’t sympathetically resonate with any note more than any other, it doesn’t sap away any energy, and it doesn’t drag the pitch of any note away from where it should be.

At least, that’s my theory. The use of graphite as neck reinforcement has become pretty commonplace, and I was happy with the results even before this weird intonation experience. Now I’m even more sold on it.

That’s all, folks!

I really think I’ve dredged up every bit of intonation information I know at this point, and I hope I’ve entertained and interested you more than annoyed and bored you with this long series of articles. But I never say never: if anyone has questions or if I haven’t been clear about something, please write me at:

http://www.doolinguitars.com/maillist.html